数学如诗,境界为上
2021-12-23 10:49:13 来源: 光明日报
王国维在《人间词话》中提出:“词以境界为最上。有境界自成高格,自有名句。”他说:“有造境,有写境,此‘理想’与‘写实’二派之所由分。”按我理解,“造境”是以意念和想象为境,“写境”是描写现实的景物。王国维还把艺术家分为“写实家”和“理想家”,并认为这两者是相通的。他还写道:“诗人对宇宙人生,须入乎其内,又须出乎其外。入乎其内,故能写之。出乎其外,故能观之。入乎其内,故有生气。出乎其外,故有高致。”
数学家维纳说:“数学是一门精美的艺术”。我认为,数学如同诗歌,评价一项数学成就,也应以境界为上。数学上也有“造境”与“写境”之分,前者是“创造理论”,后者是“解决难题”。数学家也有“写实家”和“理想家”之分,前者是“入乎其内”,侧重应用数学;后者是“出乎其外”,侧重纯粹数学,但两者是互通的。
数学与诗歌有许多共性,下面归纳为八点。
第一,数学和诗歌的源泉都是自然和社会。数学史家克莱因认为:“对自然的深入研究是数学发现最丰富的源泉。”
第二,数学和诗歌都追求和谐与简洁。诗歌是力图通过简洁的语言和韵律,抒发诗人的情怀,表达深邃的哲理。数学的和谐是不言而喻的。至于数学的简洁,一方面数学结果是通过简明的命题或定理的形式来表述的;另一方面,在研究过程中,数学家追求在较少条件下推出尽可能广泛而深刻的结论,或者力图简化已有结果的证明。
第三,数学中的“对偶”与诗词中的“对仗”是异曲同工。诗词中的“对仗”能使意境更加优美,抒情更加感人,哲理更加深邃。数学中的“对偶”使得数学理论变得更加深刻,更加优美。数学中的“对偶”不只是数学的结构和框架,而且是一种思维方式,也是重要的证明工具和技巧。
第四,数学和诗歌的创作都需要直觉和想象力。所谓直觉,就是没有经过意识推理而对某事物产生的理解和判断。当然,任何科学和艺术的创作都需要直觉和想象力,但数学和诗歌更为突出。例如,李白《望庐山瀑布》中诗句“飞流直下三千尺,疑是银河落九天”就极富直觉和想象。这种直觉和想象是源于诗人的形象思维。数学史家克莱因说:“在预测能被证明的内容时,和构思证明的方法时一样,数学家们利用高度的直觉和想象。”法国著名数学家庞加莱认为:“我们靠逻辑来证明,但要靠直觉来发明。”这里的“发明”就是指提出问题和构思证明的方法。
第五,诗歌创作和数学研究都需要激情和灵感。诗人有了激情才能把自己的感悟加深和放大,把内心情感宣泄出来,作品才能打动人和感染人。对数学研究来说,激情来自于探求未知真理的好奇和对美的追求。灵感也叫顿悟,它是一种近乎无意识或潜意识的非逻辑式的创造性思维活动。灵感是对某一问题长期思考以后突然产生的思想火花,有时产生于全神贯注思考问题之际,有时却是在不经意间或意识蒙胧之中。灵感有时也来源于对不同现象的类比和联想。
第六,数学研究和诗歌创作都需要有美感。法国数学家庞加莱在《数学创造》一文中形象地描述了数学美感在数学创造过程中的作用,他说:“各种数学概念在潜意识里碰撞组合,数学直觉从中筛选有意义的组合,进而进行创造。……潜意识做出选择时,所用的标准便是数学的美感,数和形的和谐感,几何学的雅致感。”数学史家克莱因认为:“进行数学创造的最主要驱动力是对美的追求。”
第七,“创新”是数学和诗歌的共同美学准则(即评价标准)。艺术家把“创新”叫作艺术风格。例如,李白的诗“豪迈奔放,飘逸若仙”,是浪漫主义风格;杜甫的诗则“深沉蕴蓄,抑扬曲折”,是现实主义风格。对数学研究而言,创新必须是在一定科学范围内有比较重要的意义。
第八,数学和诗歌的另一共同美学准则就是《人间词话》中所说的“境界为上”。数学的境界包括:1)大道至简,大美天成;2)简洁、和谐、对称、雅致;3)颠覆性的创新;4)交叉、融合、统一。
下面举几个高境界的数学例子。首先是两个美妙的数学公式。一是欧拉公式eiπ+1=0,它把数学里面最基本的几个要素全都整合在一块了,其中1是自然数的单位,0是正负数的分界点,e是自然对数的底,π是圆周率,i是虚数单位。二是欧拉公式V+F-E=2,公式表明:任何一个简单凸多面体,它的顶点数V加上面数F,减去棱数E必定等于2。这两个欧拉公式堪称“大道至简、大美天成”的数学公式。
数论中的三个著名猜想:“哥德巴赫猜想”(任何大于2的偶数可以表为两个素数之和)、“孪生数猜想”(存在无穷多对素数其差等于2)和“黎曼猜想”(黎曼ζ函数所有非平凡零点都位于复平面中实部为1/2的直线上),更是高境界数学的例子,尽管它们都还没有得到证明。又如庞加莱猜想、费尔马大定理、四色定理、伽罗瓦群论、黎曼几何、哥德尔不完备定理、伊藤清的随机分析、香农信息论等,这些都是属于“简洁、和谐、对称、雅致”高境界数学的例子。
20世纪50、60年代,格罗滕迪克对代数几何进行了彻底的革命,建立了“概形理论”,堪称一项颠覆性的创新。他因此于1966年获得菲尔兹奖。在概形理论基础上,数学家们取得了一系列杰出成就:1973年,德利涅证明了韦伊猜想(1978年获菲尔兹奖); 1983年,法尔廷斯证明了莫德尔猜想(1986年获菲尔兹奖);1995年,怀尔斯证明了费马大定理(1996年获菲尔兹特别奖)。
关于“交叉、融合、统一”这一数学境界,我举两个例子。其一是Atiyah-Singer指标定理:紧流形上的椭圆偏微分算子的解析指标(与解空间的维度相关)等于拓扑指标(决定于流形的拓扑性状)。其二是朗兰兹纲领,它是将数学中某些表面上毫不相干的领域(数论、代数几何与约化群表示理论)建立一种本质联系的构想。纲领是由朗兰兹在1967年给韦伊的一封信件中提出的。法籍越南数学家吴宝珠因证明朗兰兹纲领基本引理获得了2010年菲尔兹奖,朗兰兹本人获2018年度阿贝尔奖(编者注:为纪念挪威数学家尼尔斯·亨利克·阿贝尔设立的数学奖,每年颁发一次)。
我本人是研究概率论与随机分析的。我曾试图用诗歌来解析我的专业内涵,写过一首“悟道诗”:
随机非随意,概率破玄机。
无序隐有序,统计解迷离。
下面是我的另一首有关概率论的科学诗《随机与概率》,希望能引起大家对概率论的关注和兴趣。
随机与概率
熙熙人群朋友不期而遇,茫茫宇宙陨星意外撞击。
随机事件发生并非随意,概率破解其中奥秘玄机。
情境重复催生稀有事件,历史长河沉淀自然奇迹。
同班同学常有生日相同,彩民两次中奖并不神奇。
抵押贷款房产汽车按揭,精巧设计需要借助概率。
保费计算基于概率模型,期权定价有赖随机分析。
概率技巧有助破解密码,人工智能需用概率逻辑。
日常生活常遇概率问题,学点概率知识终身受益。
(作者:严加安,系中国科学院院士、中国科学院数学与系统科学研究院研究员)
为您推荐
精彩放送
热门文章
-

看好拉美业务中长期增长前景 安信国际将伟禄目标价调至18.5港元
-

陆金所控股一季度净利润同比增6.5% 八成新增借款流向小微企业
-

深圳共享单车市场或将重塑 暂不发展互联网租赁电动自行车
-

高管撑股价13家上市银行获增持 后续走势值得期待
-

A股退市名单再添两家 年内退市公司增至25家
-

年内可转债募资超千亿元 募资规模略低于去年同期
-

北交所首家转板公司诞生!观典防务在科创板上市
-

南京银行第4次被股东增持 城商行为何受“青睐”?
-

多家中小银行下调存款利率 存款降息潮是否来临?
-
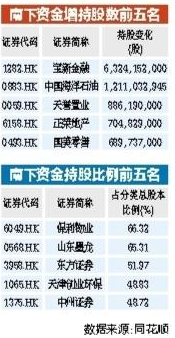
南下资金持续流入港股 年内增持中海油等43只港股逾亿股
-

降息“靴子”落地!深圳银行均已执行最新LPR报价
-

韦尔股份增持北京君正 增持后累计持有不超过5000万股
精彩图片
-

迄今最具破坏力小行星将掠过地球 飞行速度比高速飞行子弹快20倍
-

全球变暖影响人们睡眠时间 每年平均失去44小时睡眠时长
-

“下一代奇迹材料”石墨炔首创成功 填补碳材料科学空白
-

早期动物五亿多年前已形成复杂生态群落 为寒武纪大爆发奠定基础
-

西藏察隅发现中国最高树 高达83.2米胸径207厘米
-

揭示月背月壤粗细规律!月球表面年龄与月壤内部非均匀性呈正相关
-

长期暴露于野火中的居住人群 脑瘤发病率提高10%
-

研究发现:海草底部蔗糖浓度约比记录高80倍
-

4月苍穹精彩纷呈 群星“成团出道”
-

科学家发现新方法 提高鹿角珊瑚种植成功率
-

湖南首创数字贸易综合服务平台 1.2万家企业入驻
-

研究:每周吃5次或更少的肉与较低的总体癌症风险相关
热文
-

美巢专注家装环保辅料领域,致力于打造室内完美墙面
-

中视酒业供应链十大解决方案突破行业痛点多方共赢!
-

沈腾、马丽今晚做客“蘑菇屋“ 容声冰箱为新鲜美食保驾护航
-
资管机构遭仿冒,hopingclub华英会紧急澄清,请投资者提高警惕
-

QCY AilyPods蓝牙耳机预售10分钟破千台:够小够轻够性价比!
-

坚果投影仪O1和峰米R1 Nano,居家观影必备!
-
轻燃卡卡:轻体健康领域品牌林立,轻燃卡卡凭什么破圈出局?
-

数据表明母婴的风口要来了 选择靠谱的品牌是关键
-
郑明明抗皱凝时胶囊精华有效吗?要怎么用呢?
-

青海省商业性住房贷款利率下调 首套房贷利率调整为4.8%
-

太原多家楼盘已按房贷利率新标办贷 太原市民购房能省多少钱?
-

前5月兰州新区商品房销售面积环比增长约12% 价格同比增2.75%
-

5.26苏州楼市成交稳定 住宅房源共成交34367.37㎡
-

高管撑股价13家上市银行获增持 后续走势值得期待
-

A股退市名单再添两家 年内退市公司增至25家
-

银保监会拟全方位透视险企综合风险水平 全新划分风险等级
-

年内可转债募资超千亿元 募资规模略低于去年同期
-

前四月发放就业补贴超亿元 惠及高校毕业生3.8万人次
-

618选机困难症?一文读懂iQOO Neo6 SE、红米 Note 11T Pro怎么选
-

2022冰箱高峰论坛成功举办,海信真空冰箱获权威肯定
-

股票哪些技术指标最有用?如何设置股票技术指标参数?
-

深港通的标的股有哪些? 什么股票属于深港通?
-
95开头的电话能接不?9521是什么电话?
-

上折和下折什么意思? 现货折盘价是什么意思?
-

余额宝双休日也有收益吗? 零钱通周末有收益吗?
-

深发展信用卡怎么样?信用卡申请进度查询方法是什么?
-

余额宝转出10万要多久?余额宝实时到账吗?
-

乐蜂网创建时间是什么时候?乐蜂网还存在吗?
-

信用卡积分兑换订单怎么查询?5000积分兑换多少话费?
-

国美电器是做什么的董事长是谁?国美有哪些股票代码?
-
腾讯持有快手多少股票?快手与腾讯是什么关系?
-

余额宝一万块钱一天收益多少?余额宝可以当日提现吗?
-
中欧基金刘建平:优化机制和文化 提升专业能力 切实保护投资者利益
-

稻香村集团(山东公司)一行到访山东朱氏药业集团参观交流
-
蓝湾壳寡糖和壳寡糖益生菌 为您保肝护菌
-

品效双赢,“抖音520宠爱季”引领行业加倍“宠爱”
-

朱氏药业集团朱坤福:把握爆品时代机遇、迈进品牌时代新征程
-
招行信用卡借势金融科技,为客户创造更多价值
-

高新科技培育钻石,或掀时尚界新热潮
-

连续四年!用友精智成为国家级跨行业跨领域工业互联网平台
-

北交所首家转板公司诞生!观典防务在科创板上市
-

hoping club华英会成功的十个法则
-

618购游戏神机iQOO Neo6超优惠,至高24期免息+全程价保+保值换新
-

2022年新形象!AMIRO品牌全新视觉升级!
-

贵州酱酒集团“启航”,助力贵州白酒产业产业升级、产区发展
-

赛克斯发布2022年英国度假屋出租市场展望报告
-

江山欧派以动求变,实现逆势增长,2021年营收增4.84%
-

焕白新篇章,伊肤泉美白祛斑,暗沉肌再回白嫩态
-

魅力舞台 倾情演绎:宜宾天立学校举办第六届戏剧节
-

重磅发布!全景求是荣获“2021年度最佳人力资源服务机构”
